The Game

Playing the Game

• Each student needs access to a computer with an Internet connection and a Java enabled browser (running Java 2 v 1.43.x. or later.
• Game can be played during class time or at another time in which all students can commit an hour
• So far used with classes of up to 50 students; larger classes possible
• Game produces summary measures for posterior analysis and class discussion

Economic Model

Game simulates Ricardian model of trade with linear production technologies:

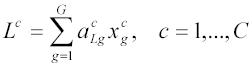
Where

 = country c’s labor endowment,

 = country c’s production of good g, and

 = unit labor requirement of good g in country c.

Consumers in all countries have the same preferences, which we model with a CES utility function

Notice that this utility function includes the logarithmic and the Leontief as limiting cases (as  approaches 0 and )

For Instructors

• Instructors can choose among the existing games or create a new one
• A game is defined by choosing country names, good names, and parameter values for 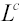,,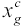 and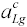  
• Typical game has 2 countries and 2 goods
• Instructors schedule the time and duration of games

If you would like to use the program, please contact Manolis Kaparakis at mkaparakis@wesleyan.edu.

For Students

• Students are randomly assigned, as they log in, to one of the countries
• The game is divided in a number of rounds, typically 4
• In each round, students decide
  • How much to produce of each good
  • Whether to post a trade
  • Whether to accept a posted trade, and
  • How much to consume of each good
• During the round, students know
  • The parameters 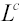and 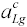 of their country
  • How their score is computed
  • Remaining time till the end of the round
  • Remaining labor endowment
  • Inventory of goods produced, offered for trade, or available to consume
  • Cumulative and current score
• The score is computed as the utility of consumption during the round
• Utility is scaled so that a value of 1 is the optimal utility under autarky; values over 1 indicate gains from trade